
Lekce 1 - šachovnice a figurky
05.01.2011 02:43 | Metodické materiály NŠAProjekt Novoborské šachové akademie Příprava vedoucích šachových kroužků mládeže realizovaný za finanční podpory Libereckého kraje je zaměřen na vznik a rozvoj šachových kroužků pro děti a mládež. Jeho součástí je i vydán
Jelikož i mezi našimi čtenáři je řada šachových trenérů a různé metodiky se mohou i výrazně lišit, uvítáme jakékoliv další podněty, které by ostatním trenérům mohly pomoci, stačí se zapojit do diskuze či poslat mail.
Obecné metodické pokyny
Jedna lekce je koncipována jako 90 minut rozdělených formálně přestávkou 10 minut do dvou bloků po 45 minutách. Případné úpravy časového plánu provede vyučující trenér v závislosti na věku posluchačů a jejich schopnosti udržet soustředění a pozornost.
Sestava lekce:
1) Opakování 10 minut - včetně kontroly domácího úkolu.
metody opakování:
a) simultánka vyučujícího - především jako test pochopení elementárních znalostí matů a koncovek
b) kontrolní test - problematika notace, pravidel, různé testovací modelové úlohy, cvičení paměti a představivosti
c) řešení úloh na diagramu - především pozdější fáze výcviku, forma soutěže, základy koncovek a taktických obratů
d) hraní tematických pozic mezi žáky - test pochopení koncovek (časově náročnější).
2) Výklad nového tématu 15 minut
metoda výkladu: demonstrace na nástěnné šachovnici. Pro malé skupinky možno využívat jen běžnou šachovnici (1 šachovnice na 2-4 žáky).
3) Procvičení nového tématu 20 minut
metody procvičování:
a) samostatné řešení podobných úloh
b) samostatné řešení modelových simulací
c) hraní tematických pozic mezi žáky
d) simultánka vyučujícího
4) Přestávka - pokud okolnosti a prostor dovolují, doporučuji pohybové aktivity
5) Přednáška na propagační téma 10 minut - různé příběhy a vyprávění vážící se k šachu, šachová historie (mistři světa a významné osobnosti historie šachu - výběr podle individuálních materiálů trenéra, doporučená temata a literatura přiloženy.
6) Výklad nového tématu 15 minutmetody výkladu viz bod 2).
7) Procvičení nového tématu 20 minut
metody procvičování viz bod 3).
8) Domácí úkol - příklady na procvičení nových témat. Rozsah úkolu podle frekvence lekcí a dosažené úrovně žáků. Doporučuji spíše menší rozsah, aby žáky neodradil od provedení úkolu, také kontrola takového úkolu nebude časově náročná. Rozsáhlejší úkoly budou zadávány před opakovací lekcí, ta bude zařazována zhruba po 6 - 8 nových tematech.
Výcvikový plán prvního cyklu:
1. Šachovnice + notace
Základní postavení šachovnice, bílý roh h1. Sloupce, řady, diagonály. Barva polí, označení polí.
2. Pravidla - tahy figur
Král - tah a braní, zvláštnosti vzájemného postavení králů, král v centru a na okraji šachovnice.
Dáma - dáma v centru a na okraji šachovnice, překážky v pohybu a působnosti
Věž - věž v centru a na okraji šachovnice, překážky v pohybu a působnosti
Střelec - střelec v centru a na okraji šachovnice, překážky v pohybu a působnosti
Jezdec - jezdec v centru a na okraji šachvice. Zvláštnosti chodu jezdce.
Pěšec - tah a braní, dvojkrok pěšce, proměna pěšce.
3. Šach, mat, pat, brani
4. Obrana před šachem, krytí figur.
5. Rošáda, braní mimochodem
6. Opakování
7. Základní taktika - dvojí úder, vazba. Krytí figury, přetížená figura, likvidace obrany.
8. Základní pěšcovky - čtverec, kritická pole, dáma proti pěšci
9. Základ zahájení partie - centrum, vývin
10. Složitější pěšcovky
11. Základní věžovky - 6. řada, most.
Lekce 1 - Šachovnice a figurky
1.1 Šachovnice

Diagram 1 - šachovnice
Šachy se hrají na hracím plánu nazývaném šachovnice, je logické, že seznámení s hrací plochou je jedním z prvních úkolů výcviku. Šachovnice je čtvercová plocha, kterou tvoří 64 čtvercových políček uspořádaných do 8 sloupců a 8 řad. Políčka pravidelně střídají bílou a černou barvu, tím vzniká barevně rozlišená síť polí, které jsou dále uspořádány do šikmých barevných diagonál.
První důležitou informací je umístění šachovnice mezi hráče: - Po pravé ruce každého hráče musí být v rohu bílé pole! - na 2. a 3. diagramu je toto pole z pohledu bílého vyznačeno zelenou barvou.

Diagram 2 - sloupce a řady
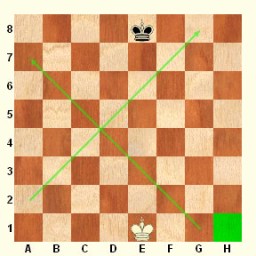
Diagram 3 - diagonály
Pro správnou orientaci na šachovnici je nezbytné zvládnout šachovou notaci - je to jakási šachová abeceda, která umožňuje jednoznačně identifikovat každé jednotlivé pole. Každý sloupec je označen písmenem abecedy v pořadí zleva (a,b,c,d,e,f,g,h), každá řada je označena číslem v pořadí od postavení bílých figur, tedy na tiskových diagramech zdola od 1 do 8. Každé pole je jednoznačně určeno dvojici těchto symbolů. Zeleně je tedy označeno krajní pole h1, sloupec b tvoří políčka b1+b2+b3+b4+b5+b6+b7+b8, třetí řadu tvoří políčka a3+b3+c3+d3+e3+f3+g3+h3. Diagonály vesměs nemají speciální pojmenování, na třetím diagramu je vyznačena diagonála a2-g8, kterou tvoří políčka a2+b3+c4+d5+e6+f7+g8, a diagonála g1-a7, kterou tvoří políčka g1+f2+e3+d4+c5+b6+a7.
Cvičení:
1. Vyhledejte zadané pole a uveďte jeho barvu: c5=černé; g6=bílé; a2=bílé; f4=černé; d8=černé; b7=bílé; e5=černé; h3=bílé.
2. Vyhledejte všechna bílá pole v těsném sousedství zadaného pole: e5=d5+f5+e4+e6; g2=f1+f3+h1+h3; a8=b7; c1=b1+c2+d1; h5=g4+g6.
3. Uveďte všechna černá pole na delší (více polí) diagonále, která prochází zadaným polem: b4=a3+b4+c6+d6+e7+f8; f2=g1+f2+e3+d4+c5+b6+a7; d7=žádné.
1.2 Figurky
Další diagram ukazuje kompletní armády obou hráčů v základním postavení.

Diagram 4 - figury v základním postavení
Obě armády mají celkem 16 kamenů rozmístěných podle diagramu. Nejpočetnější jednotkou jsou pěšci, kterých mají obě armády 8. Tito pěšci jsou seřazeni na 2. řadě (bílý), respektive na 7. řadě (černý), a oddělují tak od sebe další figury obou stran (ty stojí na 1. řadě=bílé, a na 8. řadě=černé). Nejdůležitější figurou obou stran je král, který je umístěn ve středu své armády, tedy na sloupci e (e1+e8), obklopen všemi svými spolubojovníky. Nejpohyblivější a tím i nejsilnější figurou obou stran je dáma, stojící v bezprostřední blízkosti svého krále, tedy na sloupci d (d1+d8). Pro začátečníka je užitečné zapamatovat si rčení "Dáma ctí barvu", nebude mít nikdy pochybnosti jak v základním postavení umístit krále a dámu. Bílá dáma stojí na bílém poli d1, černá dáma na černém poli d8. Po obou stranách této dvojice figur jsou umístěni 2 střelci, dále směrem k okraji šachovnice stojí v pohotovosti 2 jezdci, a na krajích obou bojových formací stojí vždy 2 mocné věže.
Pravidla šachu vyzbrojila pěšce i jednotlivé figury rozdílnými schopnosti přesunovat se po šachovnici. Každá změna postavení kamene je nazývána tah. Hráči se v provádění tahů neustále střídají, zahajovací tah provádí bílý. Poté odpovídá svým tahem černý, následuje druhý tah bílého, poté opět černý provede svůj tah, a tak dále až do konce partie. Tahem rozumíme především přemístění kamene z jednoho pole na jiné pole. Aby byl takový tah opravdu možný, nesmí na novém poli stát nějaká jiná vlastní figura. Jinými slovy, na jednom poli šachovnice může stát během celé partie vždy pouze jedna figura. Pokud na novém poli stojí soupeřův kámen, vaše figura na toto pole obvykle vstoupit může, přitom ovšem soupeřovu figuru odstraní ze šachovnice (výjimky vysvětlíme při výkladu chodu jednotlivých figur). Takový tah nazýváme braním, soupeřova odebraná figura mizí ze šachovnice a další hry již se neúčastní! Pravidla umožňují ještě dva zvláštní tahy, rošádu a braní mimochodem (tzv. an passant), o kterých budeme hovořit rovněž v souvislosti s chodem jednotlivých figur. Důležité také je, že hráč, který je na tahu, musí nějaký tah provést, nemůže se tohoto práva vzdát. Tah je totiž nejen právo, ale také povinnost. Existují situace, kdy hráč, který je na tahu, každým svým tahem svou situaci jen zhorší. Přesto však zahrát musí - takovým situacím říkáme nevýhoda tahu, v kapitolách o koncovkách se s tímto nepříjemným prvkem hry setkáme často. Pokud však hráč, který je na tahu, nemůže provést žádný tah podle pravidel, pak hra končí. Na šachovnici pak stojí buď mat, nebo pat. Mat znamená výhru partie té strany, která provedla poslední tah, pat naopak znamená nerozhodný výsledek partie. Co je mat a co je pat si vysvětlíme později.
1.2.1 Král
Již bylo řečeno, že král je nejdůležitější figurou obou armád. Je to způsobeno tím, že cílem hry je dát soupeřovu králi mat! Mat znamená, že soupeřův král je ohrožen našimi figurkami, a nemůže tomuto ohrožení čelit ani útěkem, ani braním napadající figury, ani nějakou obrannou akcí svých ostatních figur. Podrobněji o matu budeme hovořit později.

Diagram 5 - tah králem
Na tomto diagramu jsou znázorněny možné tahy jednotlivých králů. Král je figura velitelská, pravidla ho proto nijak neomezují co se týče směru jeho pohybu po šachovnici. Velitel však má mít svou důstojnost, proto se po šachovnici pohybuje zvolna a rozvážně, tedy vždy jen o jedno pole ve zvoleném směru. Tedy bílý král na poli e4 může ve svém následujícím tahu vkročit na libovolné sousední pole (d3+d4+d5+e3+e5+f3+f4+f5), všechna jsou označena zeleně. Ve svém pohybu na šachovnici má král pouze dvě omezení. Prvním omezujícím prvkem je okraj šachovnice, jak ukazuje černý král na tomto diagramu. Stojí na poli a8, což je pole na okraji šachovnice, dokonce přímo v rohu šachovnice. Král stejně jako každá jiná figura nesmí provést tah do autu, tedy mimo šachovnici. Na rozdíl od bílého krále, který může provést tah na celkem 8 různých polí, může proto černý král v následujícím tahu vstoupit pouze na 3 pole v sousedství pole a8 (a7+b7+b8). Zapamatujte si, že král na okraji šachovnice má mnohem méně svobody než král někde uprostřed šachovnice. Druhé omezení pohybu vašeho krále mohou mít na svědomí soupeřovy figury. Král totiž nesmí vstoupit na žádné pole, které je napadeno soupeřovou figurou. Zdůrazním zde skutečnost, že se to týká i polí, která napadá soupeřův král. Oba králové jsou jediné figury na šachovnici, které se během partie nikdy nemohou dostat do těsného sousedství (tj. nemohou stát na dvou sousedících polích). Asi už i vynálezce šachu věděl, že dva soupeřící velitelé se nikdy nemohou příliš přátelit. Soupeřových figur je ovšem na šachovnici mnoho, mohou tedy pohyb krále omezit velmi výrazně. Nikdy však jedna jediná soupeřova figura nemůže zbavit vašeho krále všech možností pohybu, k tomu je potřeba spolupráce nejméně dvou soupeřových figur. Král samozřejmě také nemůže vstoupit na pole, na kterém stojí vlastní figura, o tom už jsme hovořili. Pokud se však ke králi do těsné blízkosti přiblíží některá soupeřova figura, může ji král svým následujícím tahem brát jako každá jiná jeho figura. Ovšem pouze v případě, když tak král nevstoupí na ohrožené pole, tedy jinými slovy když tato soupeřova figura není kryta některou další soupeřovou figurou. Král tedy bere soupeřovy figury stejným způsobem jako provádí tah.
Pohyb krále po šachovnici nám navíc velmi dobře ukáže některé geometrické zvláštnosti šachovnice. Nejlépe si to ukážeme na následujících cvičeních:
Cvičení:
1. Projděte bílým králem po šachovnici z pole h1 na pole h8 nejkratší cestou. Kolik tahů král potřeboval?
2. Projděte bílým králem po šachovnici z pole h1 na pole c2 nejkratší cestou. Kolik tahů král potřeboval?
3. Projděte bílým králem po šachovnici z pole h1 na pole a8 nejkratší cestou. Kolik tahů král potřeboval?
4. Projděte bílým králem po šachovnici z pole h1 na pole h8 nejkratší cestou v případě, že černý král stojí na poli g5. Kolik tahů král potřeboval?
5. Projděte bílým králem po šachovnici z pole h1 na pole c2 nejkratší cestou v případě, že černý král stojí na poli f2. Kolik tahů král potřeboval?
6. Projděte bílým králem po šachovnici z pole h1 na pole a8 nejkratší cestou v případě, že černý král stojí na poli c4. Kolik tahů král potřeboval?
Přestávka
Red. pozn.: Představa, že se podaří výše uvedený výklad vyučujícímu vtěsnat do 45 minut včetně příkladů se mi jeví jako velmi optimistická, opírá se pouze o víru, že žáci již o šachu přece jen něco vědí, a že se tedy převážně hovoří o známých věcech. Procvičení správného pochopení šachové notace a procvičení chodu krále vzhledem ke geometrii šachovnice jsou ovšem významné věci, a vyučující by měl přizpůsobit časový rozvrh lekce tak, aby tato témata byla přiměřeně procvičena. Během přestávky vyučující prověří řešení cvičení tahu krále, a podle použitých řešení přizpůsobí další výklad.
Vyprávění 1 - vynález šachu a zrnka obilí
Kdysi a kdesi, nikdo neví kdy ani kde, žil mladý princ. Možná to nebyl princ, možná ani nebyl mladý, ale to není tak důležité. Byl to někdo významný, kdo si usmyslel, že ukáže, jak je chytrý. A možná vůbec nebyl, byl jen někdo velice chytrý, ale to by náš příběh zcela ztratil smysl. Takže se domluvíme, že prostě nějaký princ byl. V dávných dobách bývalo spíš potřeba, aby se princ uměl řádně ohánět klackem, kyjem, sekerou, mečem, tedy aby byl válečníkem, a na chytrost měl jiné lidi, dnes se jim říká poradci. I svolal princ své poradce a pravil: "Potřebuji někomu, to je jedno komu, dokázat, že jsem nejen lepší bojovník než on, ale že jsem také chytřejší než on. Ukládám vám proto vymyslet bojovou hru, ve které by o vítězství nerozhodoval počet ani výzbroj armád, ale jen a jen chytrost velitele té armády." Poradce jistě zalil pot. To není žádná legrace, vymyslet něco, co dosud nikdo jiný nevymyslel. Navíc když si to usmyslel pan šéf zjevně proto, aby jiným ukázal, jak je chytrý. A co když vymyslíte něco, na co inteligence pana šéfa nebude stačit, a bude v tom naopat prohrávat jednu hru za druhou? Z toho dnes kouká spíš vyhazov, v dobách tehdejších dokonce šibenice. Už jsem ale říkal, že poradce musí být chytrý, nebo alespoň mazaný. Ti princovi byli, a tak věděli, že odpovědnost bude vhodné přehrát někam dál. Vyhlásili proto na zadanou hru velký konkurs pro celý národ. Víc hlav totiž víc ví, a dobrý nápad obvykle dostane někdo, kdo si plně neuvědomuje, co všechno by z něho mohlo vzejít. Na tehdejší dobu to byl dosti neobvyklý konkurs, poradci byli rádi za každý nápad, snad ani nebrali žádné úplatky pro přijetí do konkursu. Dobře totiž věděli, že princ zadal úkol především jim samotným, a pokud se konkurs nepovede, budou v maléru. Museli být asi pěkně nervózní, princův úkol byl totiž opravdu perný, jen si zkuste sami dnes vymyslet něco podobného. Dostavilo se sice pár kandidátů, takoví se najdou vždycky, ale poradci je sami rychle vyprovodili pryč, protože nebyl takový problém rozeznat, že jejich nápady před princem neobstojí. Až se jednou dostavil nějaký chlapík, nikdo ho pořádně neznal, nikomu nebyl podobný, možná to dokonce byla žena, to se dneska také neví. Ale kdyby žil dnes, určitě bychom mu říkali génius. A předložil poradcům k posouzení hru, které říkal šachy (tenkrát to ale bylo jinou řečí, znělo to také jinak, možná šatranž, možná čaturanga, až mnohem později to snad Peršané přeložili do zvuku, který se blíží slovu šachy). Ti chytřejší poradci zajásali, a snadno své kolegy přesvědčili, že je to právě to, co potřebují. Přivedli vynálezce před prince (přece jen co kdyby se zmýlili), a princi se skutečně hra zalíbila. Vynálezce mu vysvětlil pravidla, a princ přece jen nebyl tak hloupý, aby hru nepochopil. Rozhodně si byl jist, že ji chápe lépe než ten, před kým chtěl dokázat svou chytrost. A protože chtěl ukázat také svou velkorysost, vyzval vynálezce, aby si sám určil svou odměnu. To je vskutku odvážný a hodně nerozvážný čin, který nikomu nedoporučuji opakovat, ale princ si možná říkal, že pokud si vynálezce řekne o příliš velkou odměnu, že to vyřeší nějak jinak, do hlavy mocným člověk nevidí. Zahrávat si podobným způsobem s géniem, který dokázal vynalézt šachy, se ale nevyplácí. Vynálezce se na chvilku zamyslel a pak zazněla slavná skromná věta: "Mám-li si zvolit svou odměnu, pak mi postačí zrnka pšenice. Pokryj jimi políčka této šachovnice tak, aby na prvním poli bylo 1 zrnko, na dalším poli 2 zrnka, na dalším poli pak 4 zrnka pšenice, a tak dále pokračuj, aby na každém dalším poli bylo dvakrát tolik zrnek pšenice než na poli předcházejícím, dokud nebudou pokryta všechna pole šachovnice." Princ nebyl velký znalec matematiky, a odměna se mu zdála celkem směšná, proto bez váhání souhlasil, a poručil svým poradcům, aby odměnu vyřídili. Druhý den ráno se k princi dostavil jeho hlavní poradce přes matematiku, pokrytý potem a zšedlý hrůzou (později poradci při střetu s neřešitelným úkolem páchali sebevraždy, až zase v dnešních dobách si jen začínají hledat místo poradce někoho jiného někde jinde, vývoj společnosti holt probíhá ve vývojových spirálách, ale to sem nepatří). Spočítal totiž, že by celou šachovnici musel pokrýt celkem 18 446 744 073 709 551 615 zrnky. Toto číslo si zkuste napsat na tabuli, ale nic vám to asi neřekne. Patří to do kategorie nepředstavitelných čísel. Je to prostě strašně moc. 18 trilionů a nějaké drobné, to jsou čísla, která snad někdy mohou potkat astronomové při měření vzdáleností mezi galaxiemi (vzdálenost Země od Slunce je bratru 150 milionů km, tohle číslo je o hodně řádů větší). Netuším sice, kolik zrnek pšenice představuje 1 kg, ani kolik tun pšenice se na celé zeměkouli vyprodukuje ročně, ale nemohu vyloučit, že takové množství pšenice se neurodilo na celé zeměkouli ani za poslední 2 tisíce let. Není to zase tak důležité, 2 na 63 je prostě strašlivě velké číslo, berme celý příběh jako pohádku, která snad naznačuje nekonečné možnosti šachu. A skýtá drobná poučení - nikdy nepodceňujte šachového génia, a vždycky si všechno nejdříve pořádně spočítejte.
Red. pozn.: Tento příběh má mnoho podob, drze jsem si dovolil ho poněkud převyprávět, můžete samozřejmě zvolit libovolnou vlastní verzi. Svou verzi věnuji památce dr. Jiřího Veselého, který svou knížkou "Černobílé otazníky" provázel začátečnické kroky mé vlastní šachové kariéry.
1.2.2 Geometrie šachovnice
Předcházející cvičení vám ukázala, že k překonání celé šachovnice potřebuje král celých 7 tahů. Pozoruhodné ovšem je, že pro přesun z pole h1 na pole h8 může zvolit mnoho cest, které všechny spotřebují 7 tahů: trasa h1-h2-h3-h4-h5-h6-h7-h8 spotřebuje stejný počet tahů jako například trasa h1-g2-g3-f4-e5-f6-g7-h8. První trasou se král vydal "přímo" po sloupci h, během druhé trasy si prohlédl mnohem větší plochu celé šachovnice, prošel v sousedství mnohem většího počtu polí než během první trasy, přesto však do cíle na h8 doběhl ve stejném počtu tahů. Stejný úkaz můžeme nalézt i při přesunu krále z pole h1 na pole c2, i zde je několik různých cest se shodným počtem tahů. Zato přesun krále z pole h1 na pole a8 ve třetím cvičení dává pouze jediné "nejkratší" řešení. Trasa "po diagonále" h1-g2-f3-e4-d5-c6-b7-a8 je jediná, která trvá 7 tahů (opět 7 tahů z jednoho kraje šachovnice na druhou), všechny ostatní trasy jsou o jeden nebo i více tahů delší. V matematice jste se učili, nebo se budete učit, že čtverec má všechny strany stejně dlouhé, a jeho úhlopříčka (tedy spojnice dvou nesousedících protilehlých rohů) je delší než jedna strana. Šachovnice je také čtverec, a diagonála h1-a8 je jeho "úhlopříčkou", přesto je cesta po této diagonále na počet tahů stejně dlouhá jako cesta po jedné ze stran čtverce. Zde tedy šachovnice popírá poučky matematiky či geometrie, nicméně jen částečně. Matematické pravidlo o delší úhlopříčce se projevuje tím, že cesta "po diagonále úhlopříčce" je jedna jediná, kdežto cesta po sloupci či řadě má mnoho stejně dlouhých provedení. A proč o tom vlastě mluvíme? Uložte si do paměti poznatek, že "jedinou" diagonální cestu může soupeř snadno znesnadnit a prodloužit, kdežto cestu "přímo" po sloupci může znesnadnit mnohem obtížněji. Ve cvičení 4 a 5 je postavení černého krále skutečně velkou překážkou, černý král kontroluje vždy 8 důležitých polí v oblasti, kterou musí překonat bílý král. Přesto král na g5 trasu prodlouží jen nepatrně, cesta h1-g2-f3-e4-e5-e6-f7-g8-h8 je jen o 2 tahy delší než v případě, kdy černý král na šachovnici vůbec nebyl. Černý král na f2 ovládá stejný počet polí jako král na g5, stojí velmi blízko bílého krále, jeho vliv na přesun bílého krále ve cvičení 5 je však z hlediska počtu tahů stejný, cesta h1-h2-h3-g4-f4-e4-d3-c2 trvá 7 tahů, kdežto například cesta h1-g2-f2-e2-d2-c2 trvá tahů 5, je tedy opět o 2 tahy kratší. Ve cvičení 6 naopak černý král do trasy z h1 na a8 zasahuje jen velmi málo, kontroluje sice také 8 polí, ale jen 3 z nich (d4+d5+c5) jsou ve významném kontaktu s trasou bílého krále. Bílý král se jim ale musí vyhnout, postačí krátká odbočka přes pole e5+d6. Sami si ale vyzkoušejte, jak výrazně by černý král bílému kolegovi cestu zkomplikoval, kdyby stál na poli d5, tedy přímo na nejkratší trase (jako ve cvičeních 4+5).
Vyznačte si všechny uvedené trasy na prázdné šachovnici třeba pomocí černých pěšců, a dobře si prohlédněte, jak nečekané manévry král může provádět za účelem dosažení zvoleného cíle. Později v kapitole o pěšcových koncovkách se vám toto zamyšlení určitě bude hodit.
Cvičení:
1. Cvičná hra dvojic - Královský fotbal: Bílý král na e1, černý král na e8. Hráči hrají partii jako souboj králů, branku vsítí ten, kdo dříve králem pronikne na základní řadu soupeře (tedy na 8. nebo 1. řadu). Trenér sleduje hru na všech šachovnicích, aby jednak sledoval, zda některý z žáků sám objeví klíčovou zásadu opozice králů a nevýhod tahu, a aby remízou zastavil partie, ve kterých zjevně obránce nepustí soupeřova krále dále a dochází k dlouhému opakování tahů. Po skončení partie si hráči barvy figur vymění.
2. Pokud zbývá v lekci časová rezerva, pokračuje se v procvičování šachové notace a orientace na šachovnici
Domácí úkol:
1. Určete pole všech diagonál, které procházejí polem c4.
2. Bílý král stojí na poli d1, černý král n poli f6. Určete nejkratší cestu, kterou bílý král projde nejdříve z pole e1 na pole h8, a poté z pole h8 na pole a4.
Ke stažení: Lekce 1 (pdf)
Vznik tohoto materiálu podporují:






Jen matematická poznámka:
18 446 744 073 709 551 615 = (2 na 64) - 1
na posledním políčku je 2^63 zrnek , na předposledním je 2^62 zrnek atd. na prvním je 2^0 zrnek
součet zrnek na všech políčkách je pak 2^64 - 1
P.S.
Podle wiki je předpokládáná hmotnost 461,168,602,000 tun a výška hromady zrn větší než mount everest.
Krásná práce! To se rozvoj českého šachu poměje
Jojo, taky se připojuju se svým
Super! Vynikající počin!
První lekce vypadá moc dobře!
Díky za všechny trenéry mládeže. Zdraví Jirka Majer